Summary:
My final project for ME314 was a program that used legrangian mechanics to simulate a square ball bouncing on rotating platform. The system also features a cascade controller to keep the platform stable and the ball bouncing near the center of the workspace. The simulation code in python using sympy, and the interface uses tkinter with two helper threads to run the simulation and update the GUI. The cascade controller is composed of three nested PID loops from the simple-pid package which are called each time the simulation updates. The simulation runs in near realtime, with the exception of collisions which generally take several seconds to compute.
Note (Nov 2022): I TA’d this class for Fall 2022, and touched up my final project a bit. Replacing the symbolic solve with a multi-start numerical solve got collision times down to ~0.05s which feels very nearly smooth in use.
Control Structure:
For this project I decided to try out a cascade controller (for structure see below) to set the plate torque. This structure ended up being quite easy to tune, and I would consider using it on a physical project in the future (particularly for a case like this where I want to be able to turn on each layer separately). The three controllers were chosen as follows.
The Inner PD controller was selected for greater disturbance (collision) rejection, and has much higher gains / faster feedback then the other two.
The middlemost PI controller was selected to handle the case of constant horizontal force “wind”.
The outermost controller is theoretically exposed to neither the impact disturbances (which the PD controller handles) nor the wind (which the PI controller handles) and thus works fine as just a P controller.
Collision Handling:
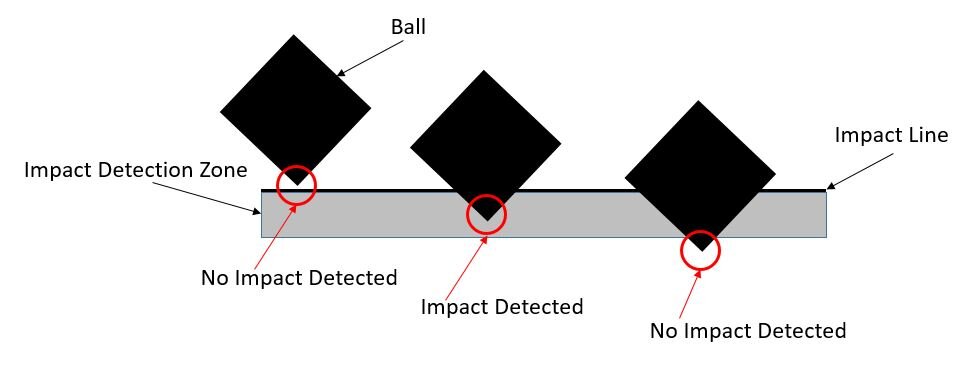
Collision detection, which is an inherently ad-hock process, is handled as shown in the figure below. The collision condition is triggered only when a ball corner fully crosses a barrier and enters the impact zone. This setup is allows for very large impact zones (since all the objects are rectangular) which reduces the chances of a corner passing through a wall without the collision being detected. Once a collision is detected, the impact equations are then solved and the relevant update is applied to the previous time step.